Zariski's main theorem

In mathematics, in the field of algebraic geometry, Zariski's main theorem is a theorem proved by Oscar Zariski that states that there is only one branch at any point of a normal variety. Informally, the reason it is true is that any branch locus is a singularity of codimension 1, while singularities of normal varieties all have codimension at least 2.

Zariski's main theorem can be stated in several ways which at first sight seem to be quite different, as there are several ways to make the informal notion of having only one branch precise. In particular the name "Zariski's main theorem" is also used for a closely related theorem of Grothendieck that describes the structure of quasi-finite morphisms of schemes, which implies Zariski's original main theorem.

The name "Zariski's main theorem" comes from the fact that it was labeled as the "MAIN THEOREM" in Zariski (1943).

Contents

Zariski's main theorem for birational morphisms

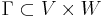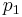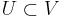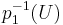Let f be a birational mapping of algebraic varieties V and W. Recall that f is defined by a closed subvariety \Gamma \subset V \times W (a "graph" of f) such that the projection on the first factor p_1 induces an isomorphism between an open U \subset V and p_1^{-1}(U), and such that 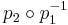p_2 \circ p_1^{-1} is an isomorphism on U too. The complement of U in V is called a fundamental variety or indeteminancy locus, and an image of a subset of V under 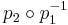p_2 \circ p_1^{-1} is called a total transform of it.

The original statement of the theorem in (Zariski 1943, p. 522) reads:

MAIN THEOREM: If W is an irreducible fundamental variety on V of a birational correspondence T between V and V′ and if T has no fundamental elements on V′ then — under the assumption that V is locally normal at W — each irreducible component of the transform T[W] is of higher dimension than W.

Here are some variants of this theorem stated using modern terminology. Hartshorne (1977) calls the following connectedness statement (Corollary III.11.4,loc.cit):

If f:X→Y is a birational projective morphism between noetherian integral schemes, then the inverse image of every normal point of Y is connected.

a "Zariski's Main theorem". The following consequence of it (Theorem V.5.2,loc.cit.) also goes under this name:

If f:X→Y is a birational transformation of projective varieties with Y normal, then the total transform of a fundamental point of f is connected and of dimension at least 1.

Zariski's main theorem for quasifinite morphisms

In EGA III, Grothendieck calls the following statement which does not involve connectedness a "Main theorem" of Zariski Grothendieck (1961, Théorème 4.4.3):

If f:X→Y is a quasi-projective morphism of Noetherian schemes then the set of points that are isolated in their fiber is open in X. Moreover the induced scheme of this set is isomorphic to an open subset of a scheme that is finite over Y.

In EGA IV, Grothendieck observed that the last statement could be deduced from a more general theorem about the structure of quasi-finite morphisms, and the latter is often refferd to as the "Zariski's main theorem in the form of Grothendieck". It is well known that open immersions and finite morphisms are quasi-finite. Grothendieck proved that under the hypothesis of separatedness all quasi-finite morphisms are compositions of such Grothendieck (1966, Théorème 8.12.6):

if Y is a quasi-compact separated scheme and 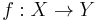f: X \to Y is a separated, quasi-finite, finitely presented morphism then there is a factorization into 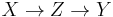X \to Z \to Y, where the first map is an open immersion and the second one is finite.

The relation between this theorem about quasi-finite morphisms and Théorème 4.4.3 of EGA III is that if f:X→Y is a projective morphism of varieties, then the set of points that are isolated in their fiber is quasifinite over Y. Then structure theorem for quasi-finite morphisms applies and yields the desired result.

Zariski's main theorem for commutative rings

Zariski (1949) reformulated his main theorem in terms of commutative algebra as a statement about local rings. Grothendieck (1961, Théorème 4.4.7) generalized Zariski's formulation as follows:

If B is an algebra of finite type over a local Noetherian ring A, and n is a maximal ideal of B which is minimal among ideals of B whose inverse image in A is the maximal ideal m of A, then there is a finite A-algebra A′ with a maximal ideal m′ (whose inverse image in A is m) such that the localization Bn is isomorphic to the A-algebra A′m′.

If in addition A and B are integral and have the same field of fractions, and A is integrally closed, then this theorem implies that A and B are equal. This is essentially Zariski's formulation of his main theorem in terms of commutative rings.

Zariski's main theorem: topological form

A topological version of Zariski's main theorem says that if x is a (closed) point of a normal complex variety then there are arbitrarily small neighborhoods U of x such that the set of non-singular points of U is connected (Mumford 1999, III.9).

Zariski's main theorem: power series form

A formal power series version of Zariski's main theorem says that if x is a point of a normal variety then the completion of the local ring at x is a normal integral domain (Mumford 1999, III.9).

See also

References